Ballistic Flight Trajectory Optimization
Problem Description
Considering a two-dimensional longitudinal profile missile trajectory optimization problem, the ballistic dynamic equation can be simplified as follows:
Among them are lift and drag, and coefficients related to aerodynamic environment.
| 气动参数 | ||||||
|---|---|---|---|---|---|---|
| 值 | 497 (kg) | 7.6 (m) | 0.3(m) | 0.0707() | 0.53 | 11.78 |
The optimization objective comprehensively considers overload (least squares) integration and maximizing end velocity, and the OCP model is defined as:
Modeling
NN = 100
prob = multi_stage_problem('ballistic_flight', NN + 1)
""" Provide Auxiliary Data for Problem """
D = 0.3
S = 0.25 * pi * D ** 2 # Vehicle Reference Area (mˆ2)
rho0 = 1.225570827014494 # Sea Level Atmospheric Density (kg/mˆ3)
beta = 1.208e-4
mass0 = 812.0
m_pulse = 333.0
mass = mass0 - m_pulse # Vehicle Mass (kg)
Cx0_s = 0.53
CN_alpha_s = 11.78
""" Boundary Conditions """
speed0, fpa0, range0, alt0 = prob.parameters(['speed0', 'fpa0', 'range0', 'alt0'], stage_dependent=False)
fpaf, rangef, altf = prob.parameters(['fpaf', 'rangef', 'altf'], stage_dependent=False)
tfWeight, vfWeight, uWeight = prob.parameters(['tfWeight', 'vfWeight', 'uWeight'], stage_dependent=False)
""" Limits on Variables """
tfMin, tfMax = 40.0, 880.0
rangeMin, rangeMax = 0, 200000
altMin, altMax = -40000.0, 0.0
speedMin, speedMax = 250.0, 2500.0
anMin, anMax = -20.0, 20.0
fpaMin, fpaMax = -90.0 * pi / 180.0, 90.0 * pi / 180
aoaMin, aoaMax = -10.0 * pi / 180.0, 10.0 * pi / 180.0
V = prob.variable('V', hard_lowerbound=speedMin, hard_upperbound=speedMax)
gamma = prob.variable('gamma', hard_lowerbound=fpaMin, hard_upperbound=fpaMax)
l = prob.variable('y', hard_lowerbound=rangeMin, hard_upperbound=rangeMax)
y = prob.variable('l', hard_lowerbound=altMin, hard_upperbound=altMax)
tf = prob.variable('tf', hard_lowerbound=tfMin, hard_upperbound=tfMax)
aoa = prob.variable('aoa', hard_lowerbound=aoaMin, hard_upperbound=aoaMax) # aoa
""" Compute the Aerodynamic Quantities """
CD = 0.5 * rho0 * S * Cx0_s
CN = -0.5 * rho0 * S * CN_alpha_s # lift coefficient
Fl = CD * exp(-beta * y) * V * V
Fy = CN * exp(-beta * y) * V * V * aoa
gravity = 9.81
""" Evaluate Right-Hand Side of the Dynamics """
vdot = (-Fl + Fy * aoa) / mass - gravity * sin(gamma)
gammadot = (-Fy - mass * gravity * cos(gamma)) / (mass * V)
ldot = V * cos(gamma)
ydot = V * sin(gamma)
dynamics = [vdot, gammadot, ldot, ydot, 0]
ts = tf / NN
ode = differential_equation(
state=[V, gamma, l, y, tf],
state_dot=dynamics,
stepsize=ts,
discretization_method='forward_euler')
prob.equality(ode)
obj_u = general_objective(uWeight * aoa ** 2)
prob.objective(obj_u)
obj = general_objective(-vfWeight * V + tfWeight * tf)
# maximize range
prob.end_objective(obj)
seq = general_equality([V - speed0, gamma - fpa0, l - range0, y - alt0])
prob.start_equality(seq)
eeq = general_equality([gamma - fpaf, l - rangef, y - altf])
prob.end_equality(eeq)
# amin <= a <= a_max
an = V * gammadot / gravity
ineq = general_inequality(
expr = [an, an],
sign = ['>=', '<='],
bound = [anMin, anMax])
prob.inequality(ineq)
option = codegen_option()
codegen = code_generator()
codegen.codegen(prob, option)
Solution
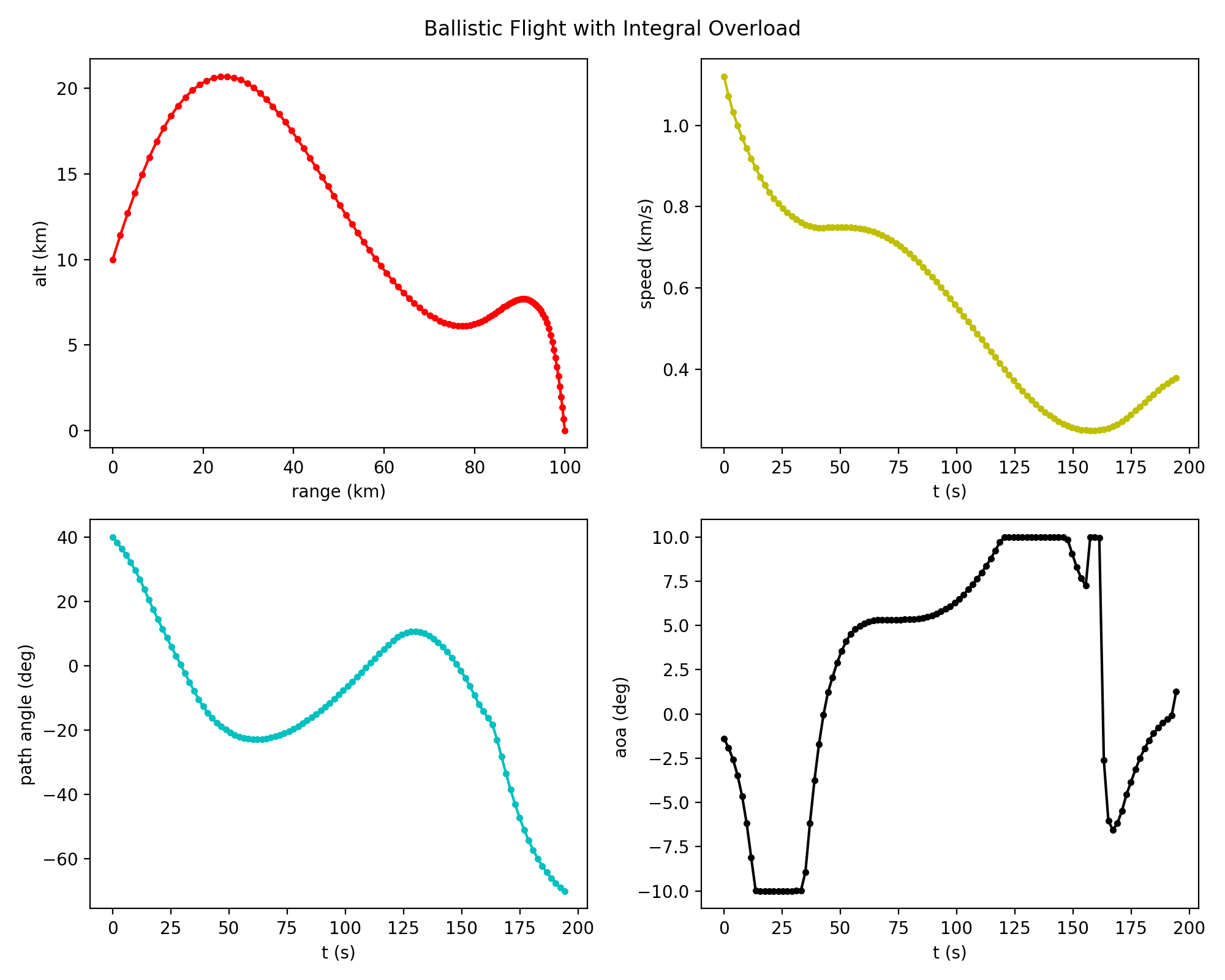
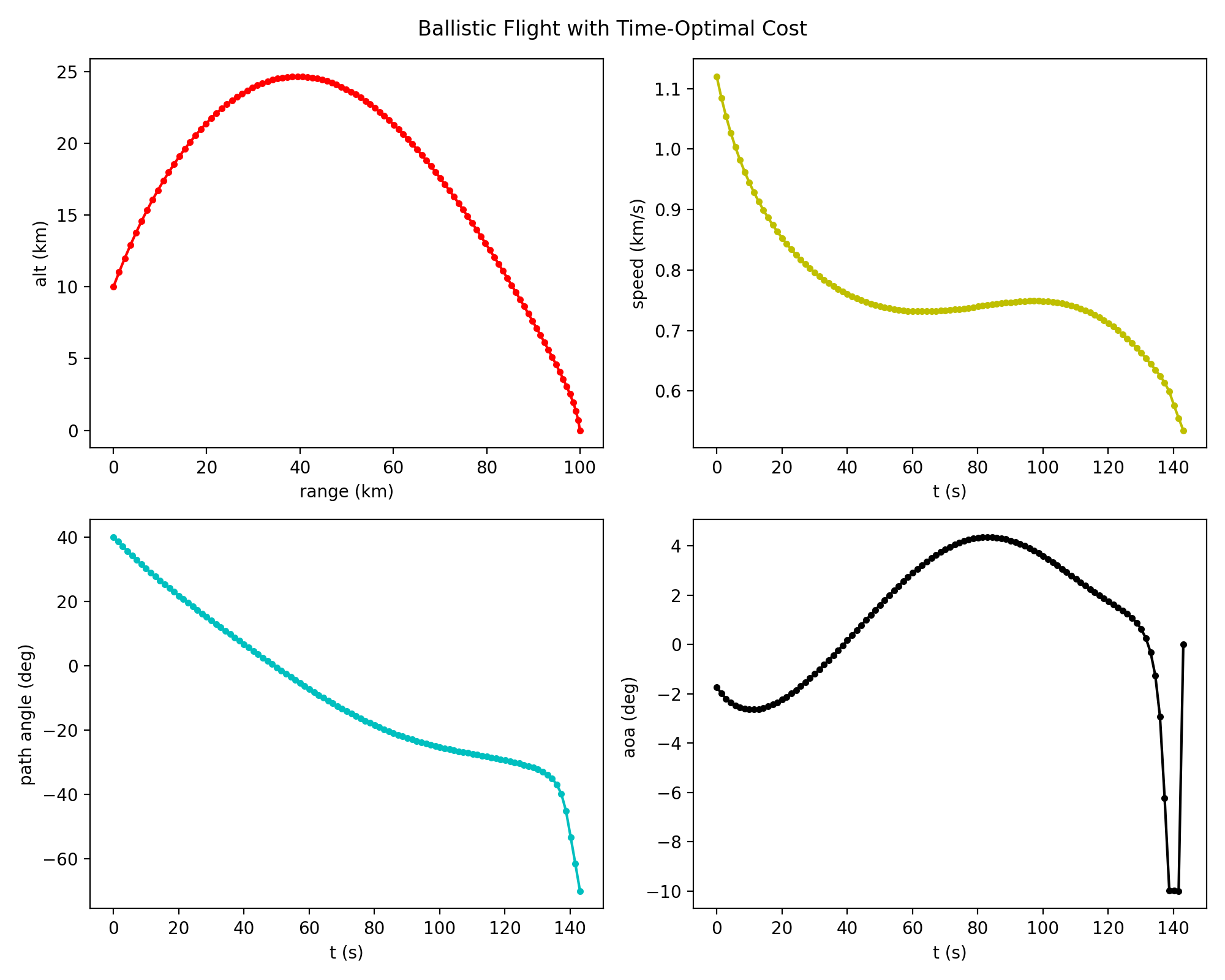

[1]. 聂万胜, 冯必鸣, 李柯. 高速远程精确打击飞行器方案设计方法与应用. 国防工业出版社, 2014.