速度规划问题 - 扩展模型
在上述例子中, 我们考虑了简单的速度规划问题的建模与求解. 下面我们将模型扩展为一个更复杂的模型:
- 考虑控制量的变化率约束/惩罚
- 考虑变量的耦合约束
- l1范数的目标函数
变化率约束/惩罚
假设控制量的变化率的约束为[-5, 5] . 同时, 我们需要在目标函数中添加控制量变化率的惩罚项.
我们可以引入控制量的高阶导数变量来表示控制量的变化率. 然后对于变量, 我们设置其上下界为[-5, 5] , 并且对其进行惩罚.
新增变量:
jerk = prob.variable('jerk', hard_lowerbound=-5, hard_upperbound=5)
目标函数变更为:
obj = general_objective((v - vref)**2 + 0.1 * jerk**2)
prob.objective(obj)
约束条件变更为:
ode = differential_equation(
state=[s, v, a],
state_dot=[v, a, jerk],
stepsize=0.1,
discretization_method='erk4')
prob.equality(ode)
初始条件变更为 (增加了加速度的初始值约束):
seq = general_equality([s - 0, v - 0, a - 0])
prob.start_equality(seq)
效果如下:
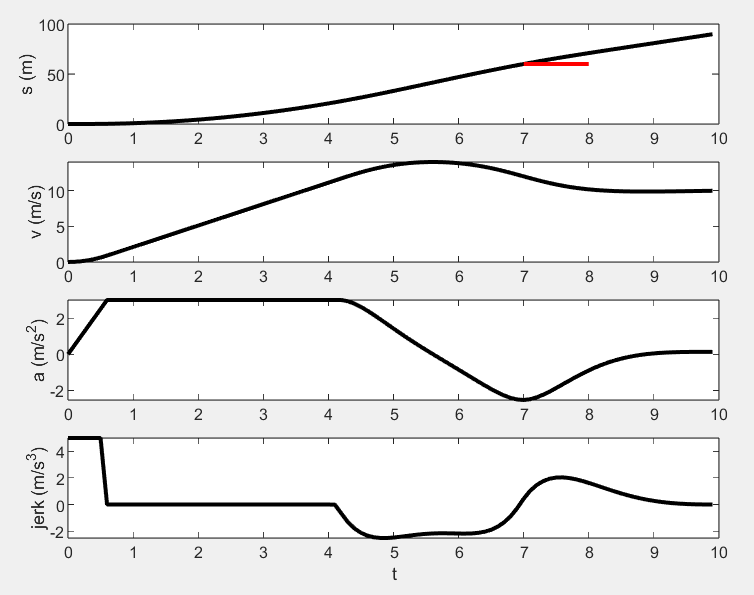
耦合约束
假设我们需要在[7, 8] s的时间窗口内, 希望距离约束保留一定的随速度变化的裕度:
这里我们使用了general_inequality函数来定义耦合约束.
tsafe = prob.parameter('tsafe', stage_dependent=True)
ineq = general_inequality([s - tsafe * v - smin], sign=['>='], bound=[0.0])
prob.inequality(ineq)
同样, 在求解时, 我们需要设置[7, 8] s间的tsafe的值为0.2.
for (size_t i = 0; i < SPEED_PLANNING_DIM_N; i++) {
/* smin, tsafe */
if ((i >= 70) && (i <= 80)) {
prob.param_stage[i][SPEED_PLANNING_PARAM_STAGE_SMIN] = 60.0;
prob.param_stage[i][SPEED_PLANNING_PARAM_STAGE_TSAFE] = 0.2;
} else {
prob.param_stage[i][SPEED_PLANNING_PARAM_STAGE_SMIN] = 0.0;
prob.param_stage[i][SPEED_PLANNING_PARAM_STAGE_TSAFE] = 0.0;
}
}
效果如下:
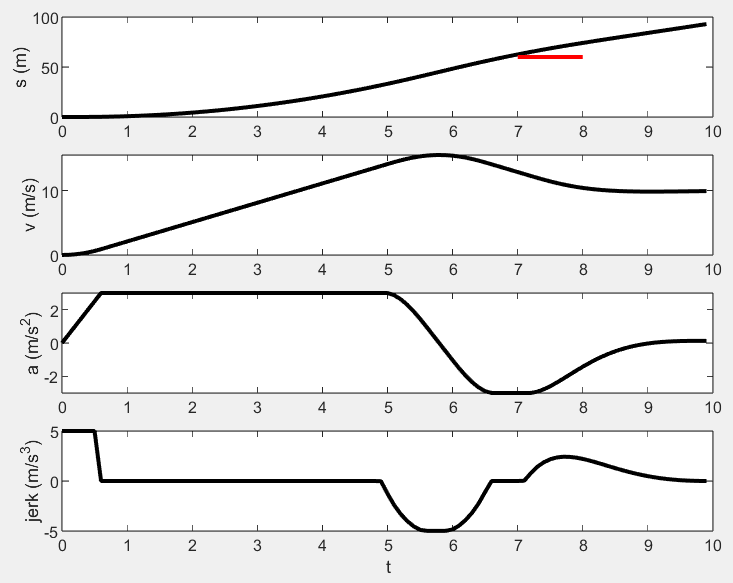
l1范数的目标函数
假设我们需要将目标函数变更为l1范数的形式:
注意, 上述目标函数不是一个smooth的目标函数, 我们需要对其进行等效转化. 通过引入slack变量与, 上述目标函数可以转化为:
同时, 我们需要添加以下的约束条件:
对于上述优化问题, 我们可以使用OPTIMake内置的软约束接口等效实现. 这样我们就不需要显示地定义slack变量, 实现内存占用与计算时间的减少.
对于变量, 上述可以等效于一个上下限都为0的l1软约束:
jerk = prob.variable('jerk', hard_lowerbound=-5, hard_upperbound=5,
soft_lowerbound=0, soft_upperbound=0,
weight_soft_lowerbound=0.1, weight_soft_upperbound=0.1,
penalty_type_soft_lowerbound='l1',
penalty_type_soft_upperbound='l1')
对于变量, 上述也可以等效于一个上下限都为0的l1软约束:
ineq = general_inequality([s - tsafe * v - smin, v - vref, v - vref],
sign=['>=', '>=', '<='],
bound=0.0)
prob.inequality(ineq, penalty_type=['none', 'l1', 'l1'], weight_soft=[inf, 1.0, 1.0])
效果如下, 可以看到l1范数的目标函数与二次型的目标函数相比, 可以使得加减速更加线性.
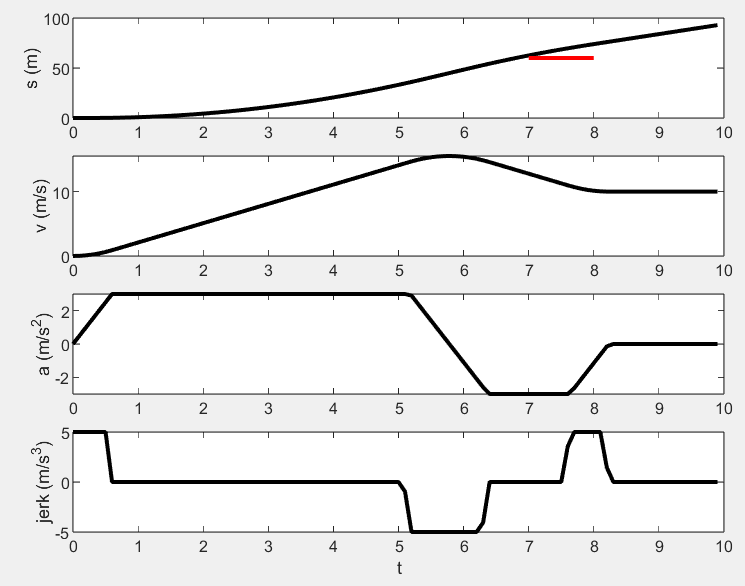
附录
以上建模的完整代码如下:
prob = multi_stage_problem('speed_planning', 100)
vref = prob.parameter('vref', stage_dependent=False)
smin = prob.parameter('smin', stage_dependent=True)
tsafe = prob.parameter('tsafe', stage_dependent=True)
s = prob.variable('s', hard_lowerbound=smin)
v = prob.variable('v')
a = prob.variable('a', hard_lowerbound=-3, hard_upperbound=3)
jerk = prob.variable('jerk', hard_lowerbound=-5, hard_upperbound=5,
soft_lowerbound=0, soft_upperbound=0,
weight_soft_lowerbound=0.1, weight_soft_upperbound=0.1,
penalty_type_soft_lowerbound='l1',
penalty_type_soft_upperbound='l1')
# use differential equation to define the state equation
ode = differential_equation(
state=[s, v, a],
state_dot=[v, a, jerk],
stepsize=0.1,
discretization_method='erk4')
prob.equality(ode)
# alternative way to define the state equation
# h = 0.1
# dis_eq = discrete_equation(
# expr_next_stage=[s, v, a],
# expr_this_stage=[s + h * v + 0.5 * h**2 * a + 1/6 * h**3 * jerk,
# v + h * a + 0.5 * h**2 * jerk,
# a + h * jerk],
# )
# prob.equality(dis_eq)
ineq = general_inequality([s - tsafe * v - smin,
v - vref, v - vref],
sign=['>=', '>=', '<='], bound=0.0)
prob.inequality(ineq, penalty_type=['none', 'l1', 'l1'], weight_soft=[inf, 1.0, 1.0])
seq = general_equality([s - 0, v - 0, a - 0])
prob.start_equality(seq)
option = codegen_option()
codegen = code_generator()
codegen.codegen(prob, option)
以上求解的完整代码如下:
#include "speed_planning_prob.h"
#include "speed_planning_solver.h"
#include <stdio.h>
int main(void)
{
Speed_planning_Problem prob;
Speed_planning_Option option;
Speed_planning_WorkSpace ws;
Speed_planning_Output output;
speed_planning_init(&prob, &option, &ws);
/* params */
prob.param[SPEED_PLANNING_PARAM_VREF] = 10.0; /* vref */
for (size_t i = 0; i < SPEED_PLANNING_DIM_N; i++) {
/* smin, tsafe */
if ((i >= 70) && (i <= 80)) {
prob.param_stage[i][SPEED_PLANNING_PARAM_STAGE_SMIN] = 60.0;
prob.param_stage[i][SPEED_PLANNING_PARAM_STAGE_TSAFE] = 0.2;
} else {
prob.param_stage[i][SPEED_PLANNING_PARAM_STAGE_SMIN] = 0.0;
prob.param_stage[i][SPEED_PLANNING_PARAM_STAGE_TSAFE] = 0.0;
}
}
/* option */
int solve_status = speed_planning_solve(&prob, &option, &ws, &output);
printf("solve_status = %d\n", solve_status);
return 0;
}