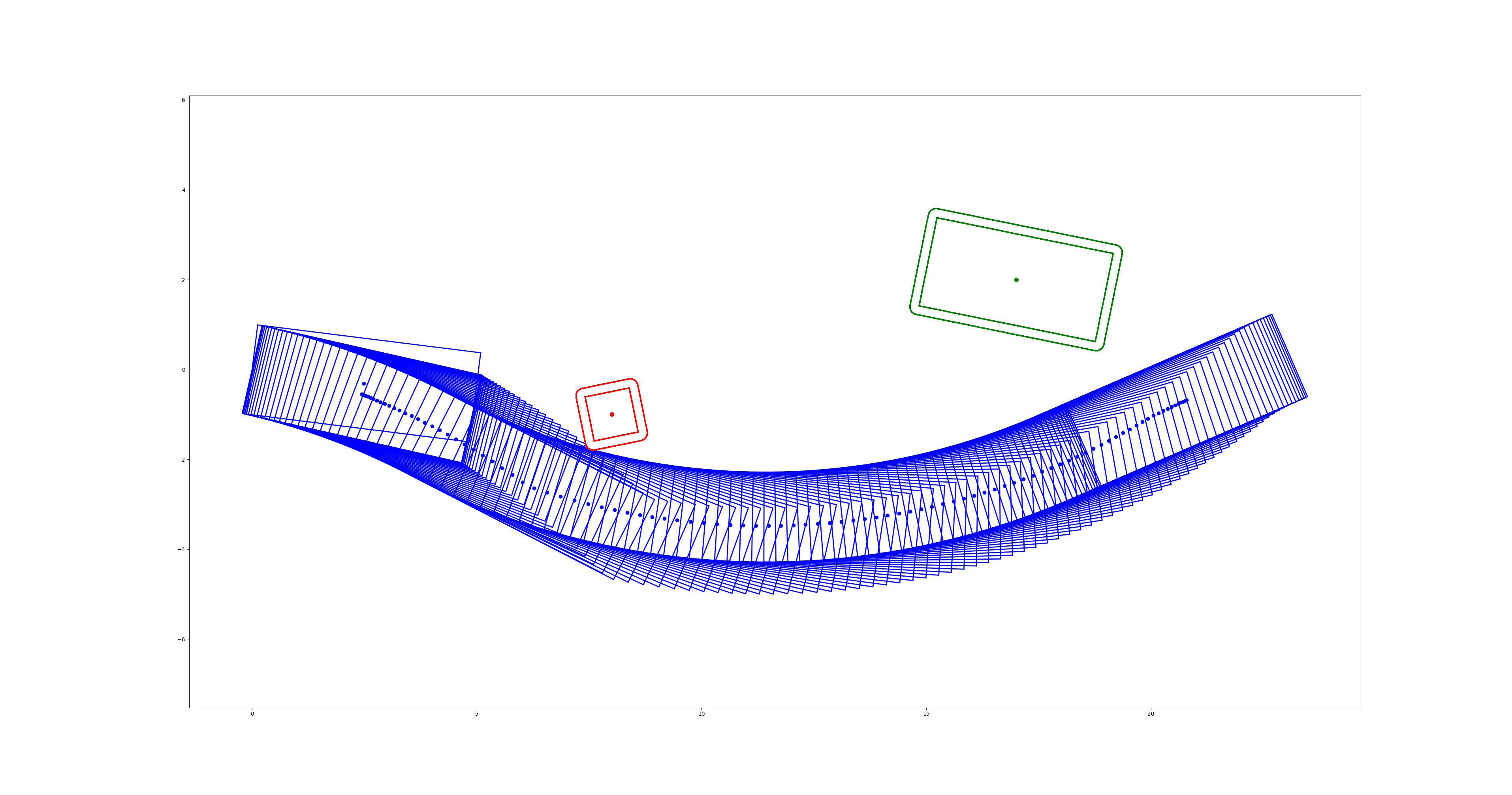
Collision avoidance
OPTIMake实现了对几何图形避障约束的直接支持, 可通过建模接口直接定义避障不等式约束, 支持以下类型的避障不等式约束:
point_to_rectangle_inequality: 点对矩形的避障不等式约束rectangle_to_rectangle_inequality: 矩形对矩形的避障不等式约束
在使用前需要先导入相关的接口:
from optimake.extension.collision_avoidance import *
避障约束为非凸约束, 根据初始解的设置, 可能会导致求解器陷入不同的局部最优解
OPTIMake并不要求初始解为满足避障约束的可行解, 但当初始解具备清晰的避障模态时, 求解结果的避障模态一般会与初始解避障模态保持一致. 例如在车与车避障中, 当初始解为A车在B车的左侧时, 求解结果的A车轨迹通常也会在B车的左侧
反之当避障模态不清晰时, 求解结果的避障模态可能会与初始解避障模态不一致, 甚至可能导致求解不收敛. 例如A车与B车的初始解重叠时, 避障模态不清晰, 求解模态可能会在A车与B车的左侧或右侧, 甚至可能会导致求解不收敛
point_to_rectangle_inequality
建模
下面为点对矩形的避障不等式约束的例子:
point2rect_ineq = point_to_rectangle_inequality(
px, py,
x, y, phi, width, length,
distance_to_avoid
)
prob.inequality(point2rect_ineq)
其中, point_to_rectangle_inequality接口的入参如下:
px,py: 点的坐标x,y,phi: 矩形的中心坐标和朝向 (逆时针为正)width,length: 矩形的宽度和长度distance_to_avoid: 避障距离
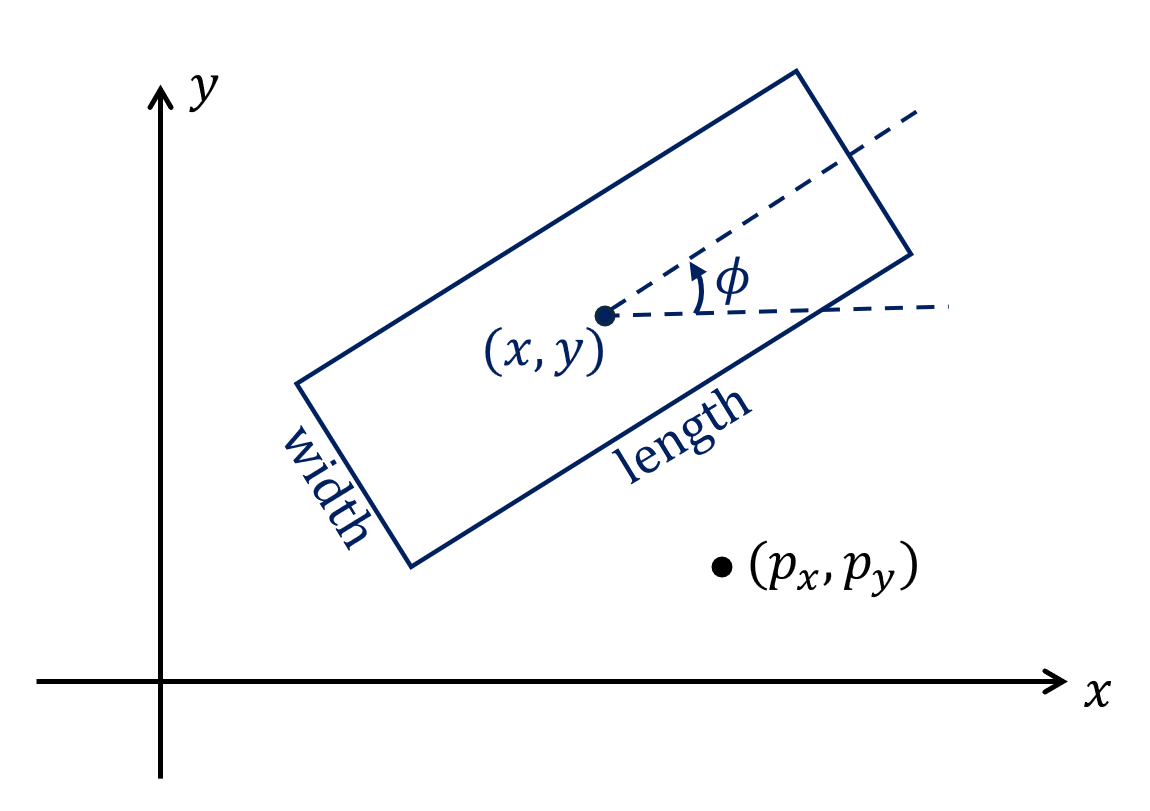
width, length可以为常数, 或者关于参数的表达式. 而其余参数 (px, py, x, y, phi, distance_to_avoid)可以为常数, 关于参数的表达式, 或者关于优化变量的表达式
效果
下面为利用点对矩形的避障功能实现的车辆避障轨迹规划的问题设定:
- 车辆起始位姿为0, 目标为跟踪x轴 (横轴)的参考线并且避开两个人 (通过点描述)
- 车辆的优化轨迹为100个stage, 每个stage, 即每个时间点处的车辆都与两个点进行避障, 避障距离为1.0 m
注意, 人在不同时间点处的位置可以不同, 即可处理动态避障问题.
下面为不同初始解下的轨迹规划效果图:
- 初始解在上方
- 初始解在中间
- 初始解在下方
初始解:
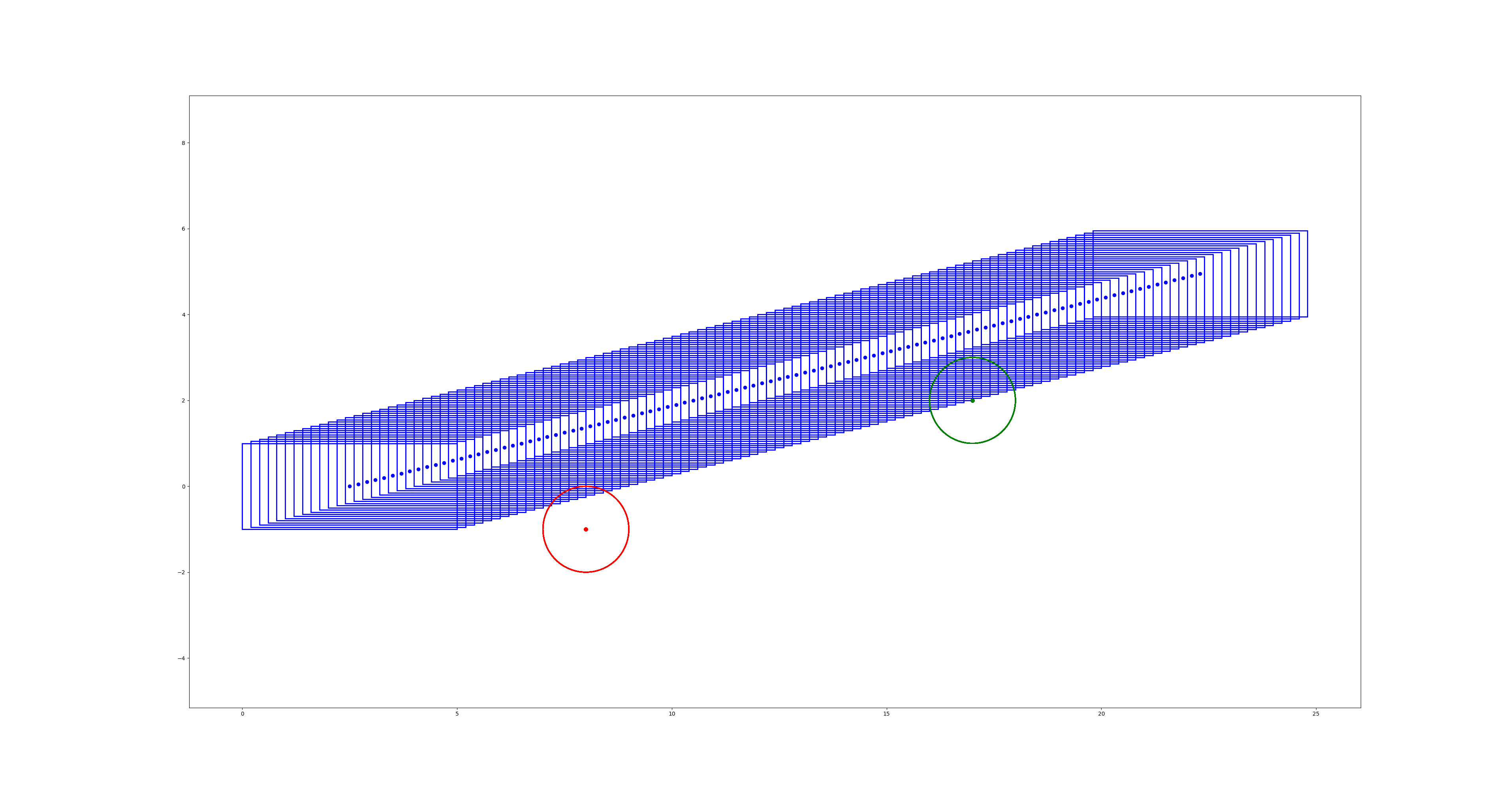 最优轨迹:
最优轨迹:
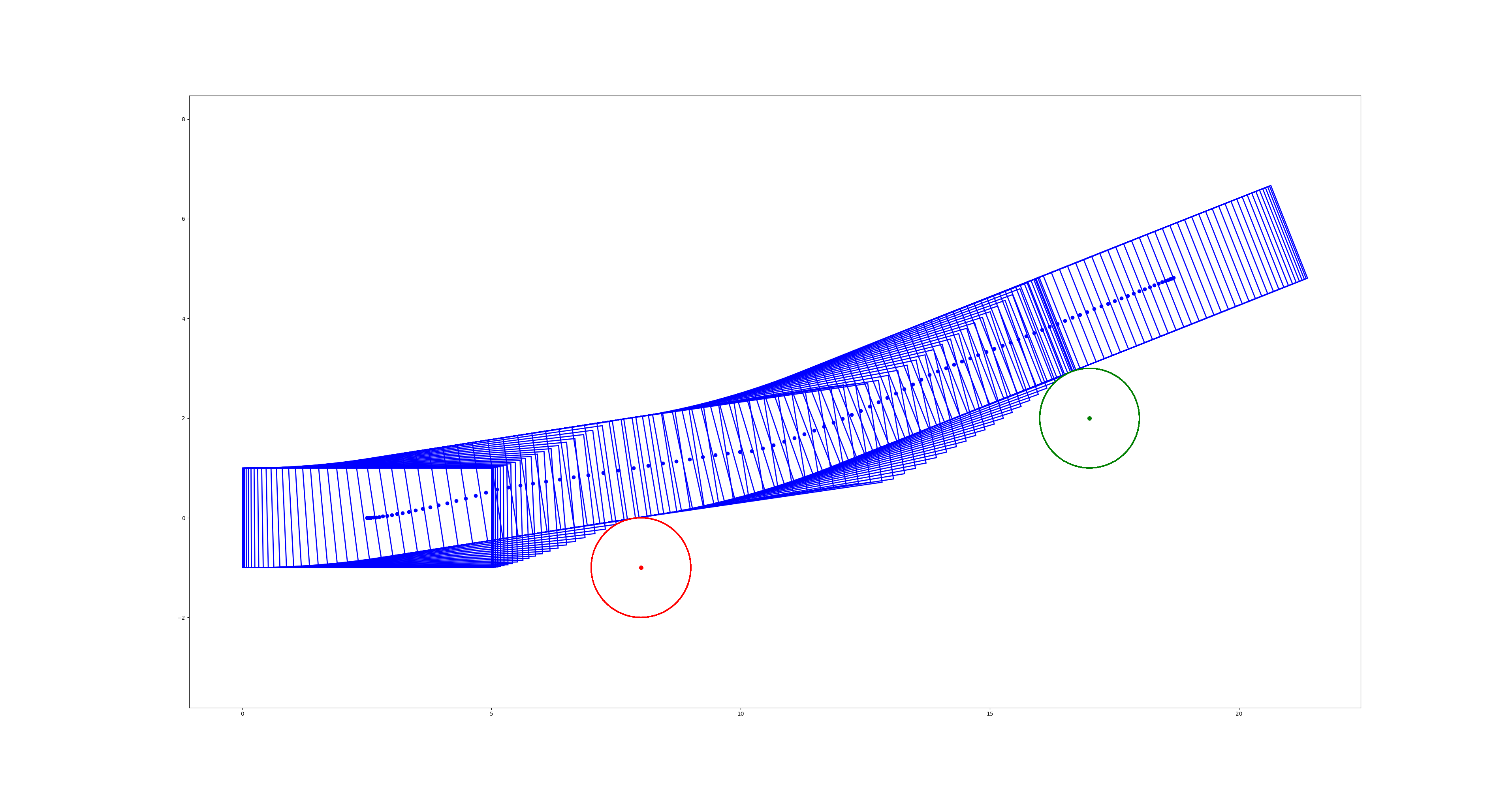
初始解:
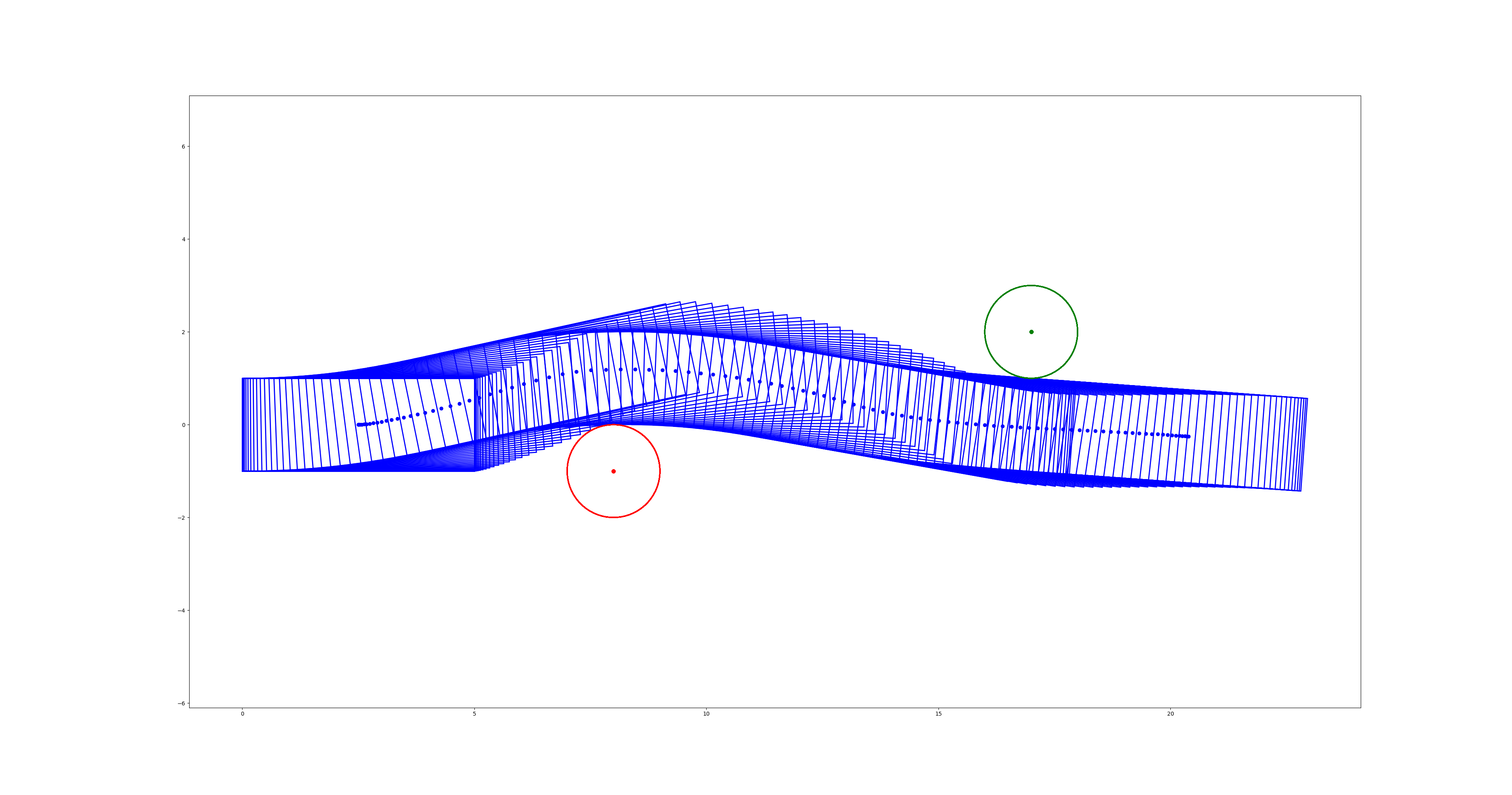
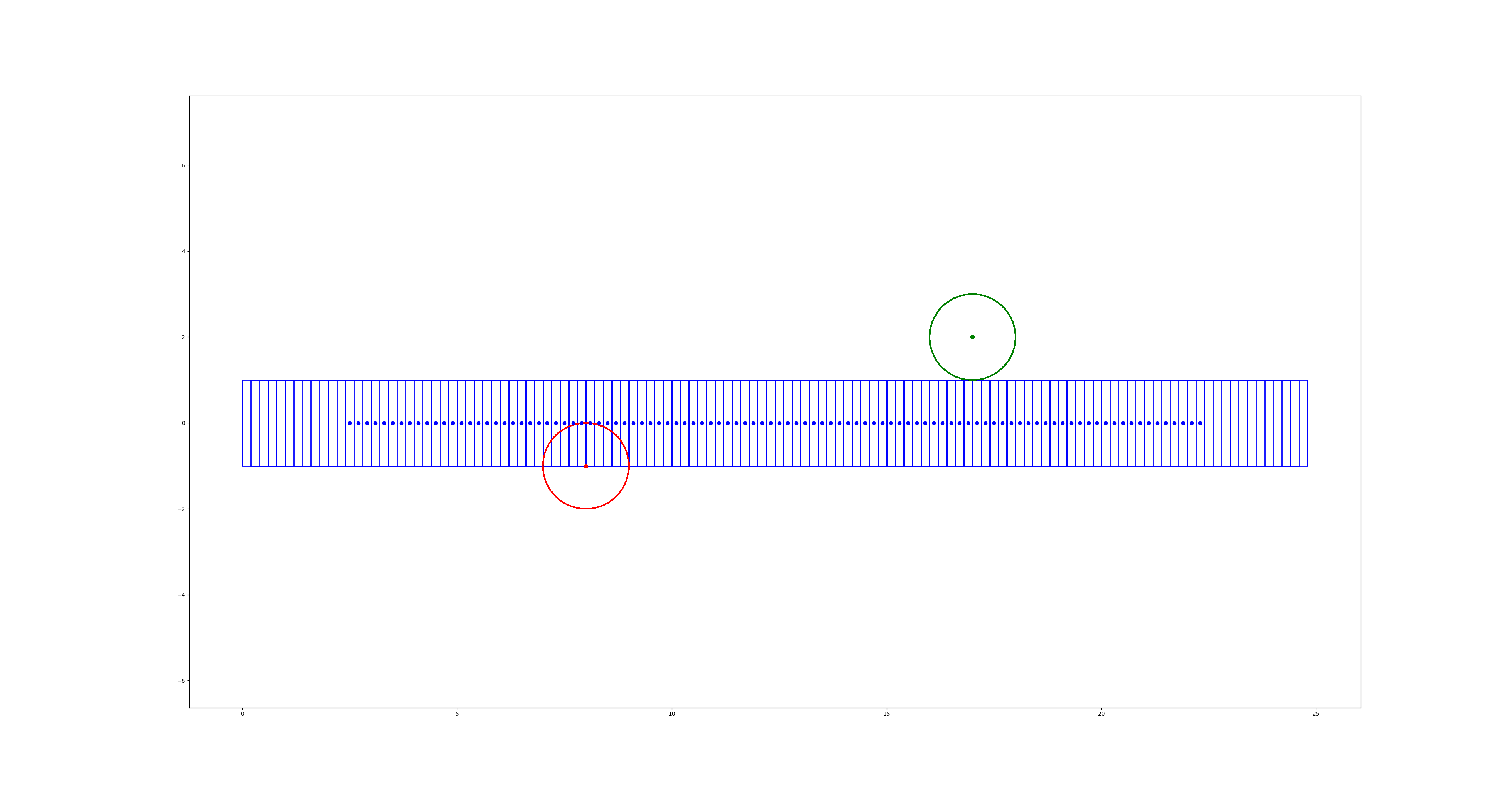 最优轨迹:
最优轨迹:
初始解:
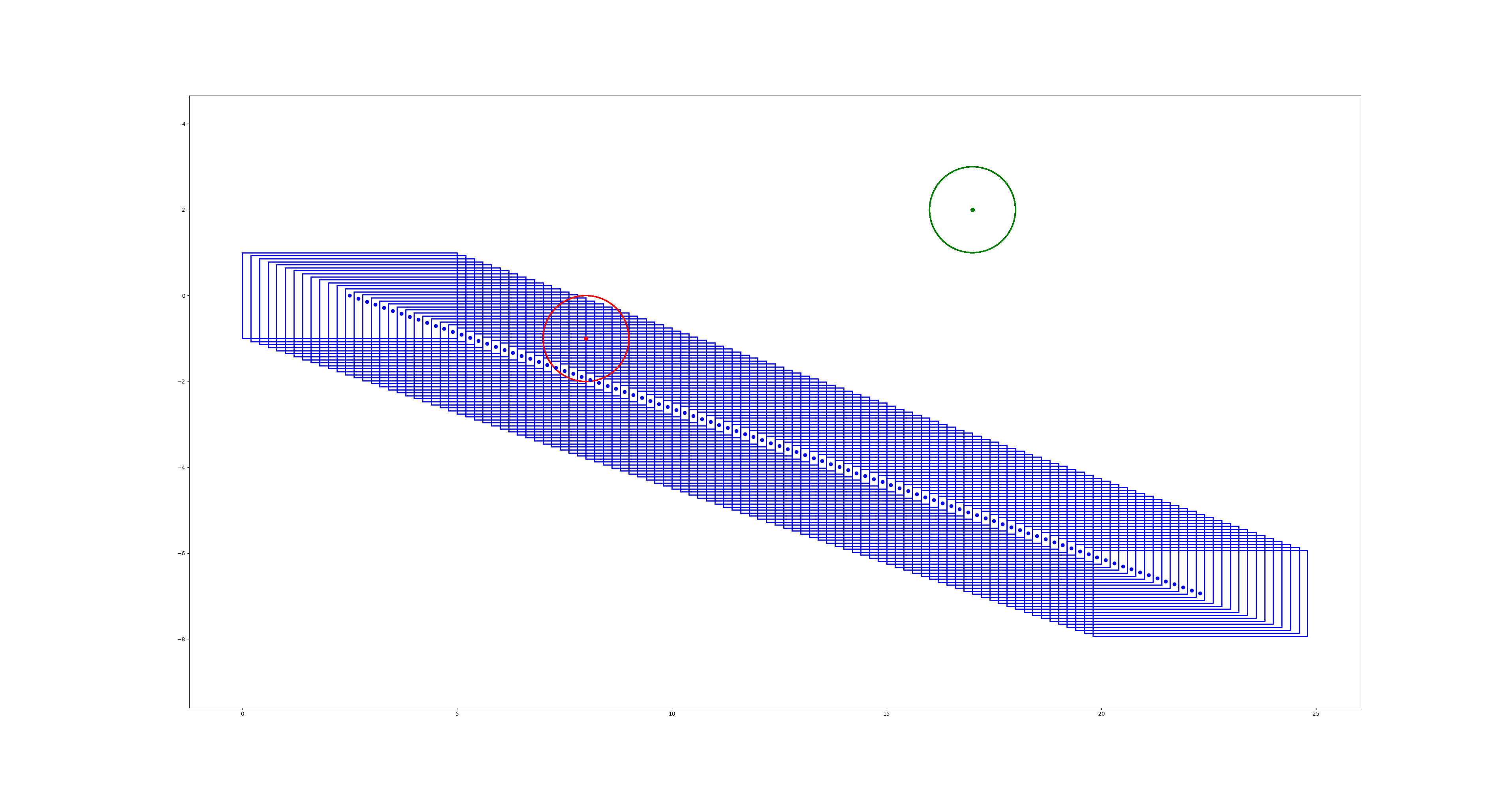 最优轨迹 (受最大转角约束限制, 求解器返回
最优轨迹 (受最大转角约束限制, 求解器返回solve_status = 3的不可行标志位与最小约束违反解):
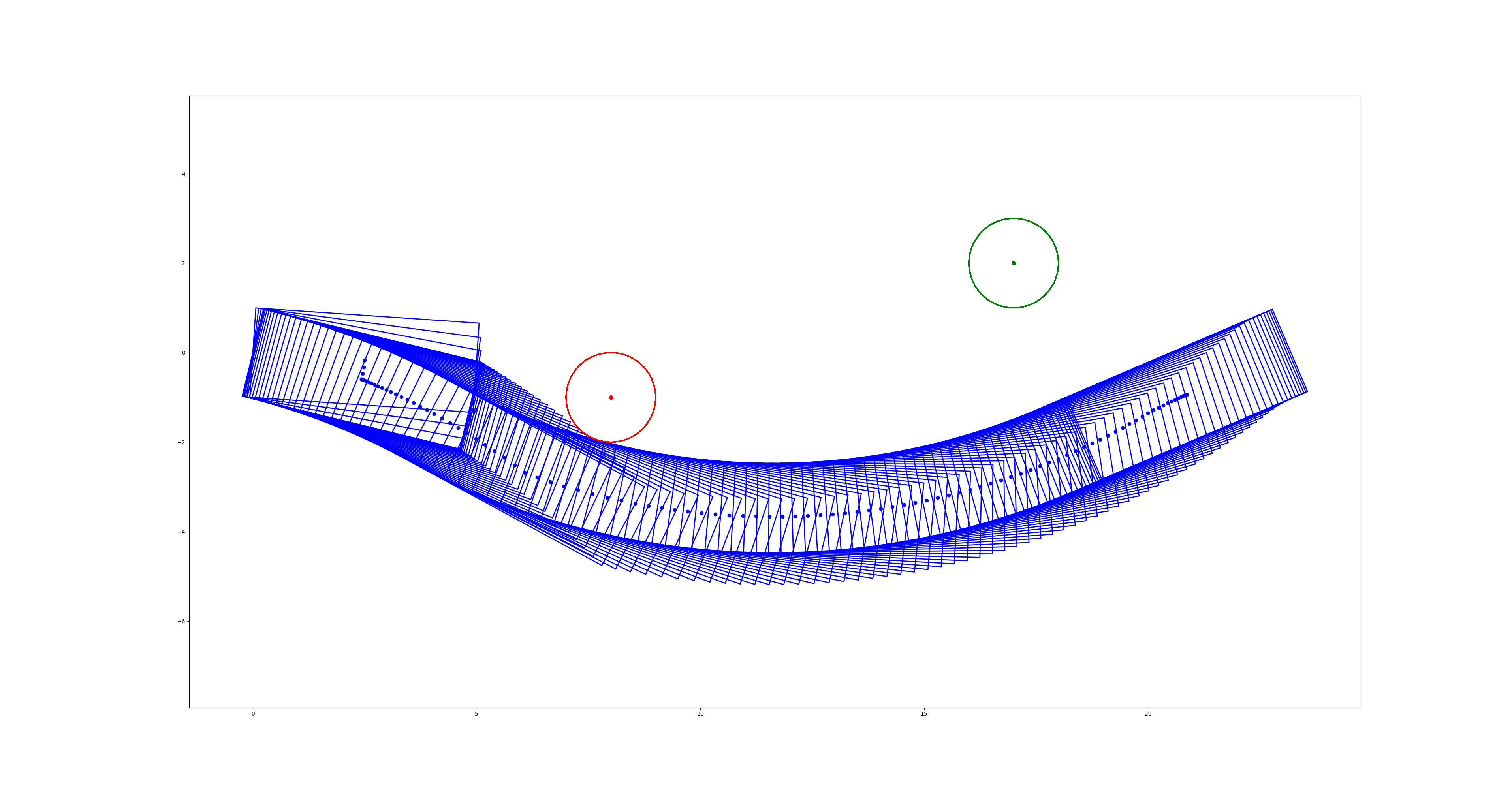
rectangle_to_rectangle_inequality
建模
下面为矩形对矩形的避障不等式约束的例子:
rect2rect_ineq = rectangle_to_rectangle_inequality(
x_a, y_a, phi_a, width_a, length_a,
x_b, y_b, phi_b, width_b, length_b,
distance_to_avoid,
center_point_avoidance
)
prob.inequality(rect2rect_ineq)
其中, rectangle_to_rectangle_inequality接口的入参如下:
x_a,y_a,phi_a: 矩形a的中心坐标和朝向 (逆时针为正)width_a,length_a: 矩形a的宽度和长度x_b,y_b,phi_b: 矩形b的中心坐标和朝向 (逆时针为正)width_b,length_b: 矩形b的宽度和长度distance_to_avoid: 避障距离center_point_avoidance: 是否对矩形的中心点进行避障 (默认为True, 即对中心点进行避障). 当为True时, 会增加矩形a的中心点对矩阵b的避障约束与矩形b的中心点对矩形a的避障约束, 避障距离分别为distance_to_avoid + min(width_a, length_a) / 2(即矩形a的中心点与矩形b之间的距离需要大于避障距离加上矩形a的半宽度或半长度) 与distance_to_avoid + min(width_b, length_b) / 2
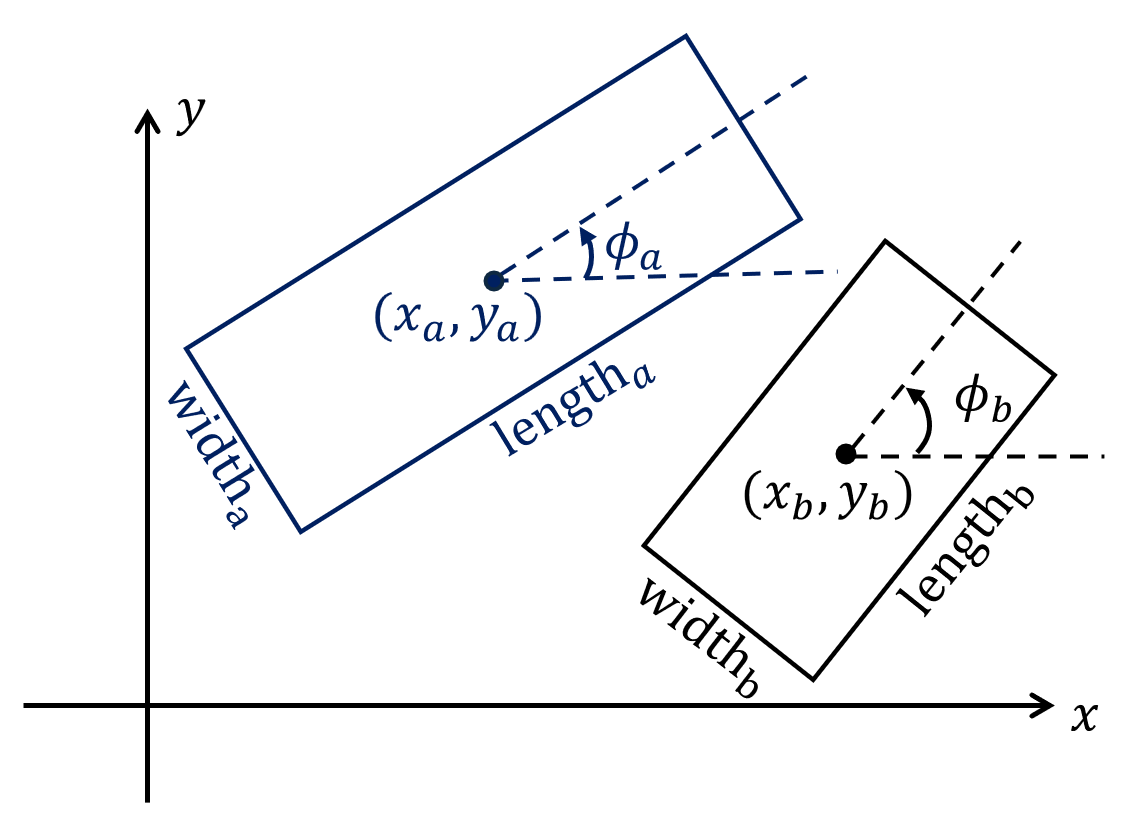
width_a, length_a, width_b, length_b可以为常数, 或者关于参数的表达式. 而其余参数 (x_a, y_a, phi_a, x_b, y_b, phi_b, distance_to_avoid)可以为常数, 关于参数的表达式, 或者关于优化变量的表达式
rectangle_to_rectangle_inequality的原理为构建8个point_to_rectangle_inequality约束, 其中4个约束为矩形a的四个角点对矩形b的避障约束, 4个约束为矩形b的四个角点对矩形a的避障约束- 该约束不能处理矩形a与矩形b重叠且各自的四个角点在对方矩形外部的情况 (例如十字交叉的情况), 可以通过设置
center_point_avoidance为True添加中心点��的point_to_rectangle约束来减少这种情况的发生, 或者可以自行添加其他点处的point_to_rectangle约束来处理这种情况
效果
下面为利用矩形对矩形的避障功能实现的车辆避障轨迹规划的问题设定:
- 车辆起始位姿为0, 目标为跟踪x轴 (横轴)的参考线并且避开两个其他车辆
- 车辆的优化轨迹为100个stage, 每个stage, 即每个时间点处的车辆都与两个其他车辆进行避障, 避障距离为0.2 m
注意, 其他车辆在不同时间点处的位置可以不同, 即可处理车辆间的动态避障问题.
下面为不同初始解下的轨迹规划效果图:
- 初始解在上方
- 初始解在中间
- 初始解在下方
初始解:
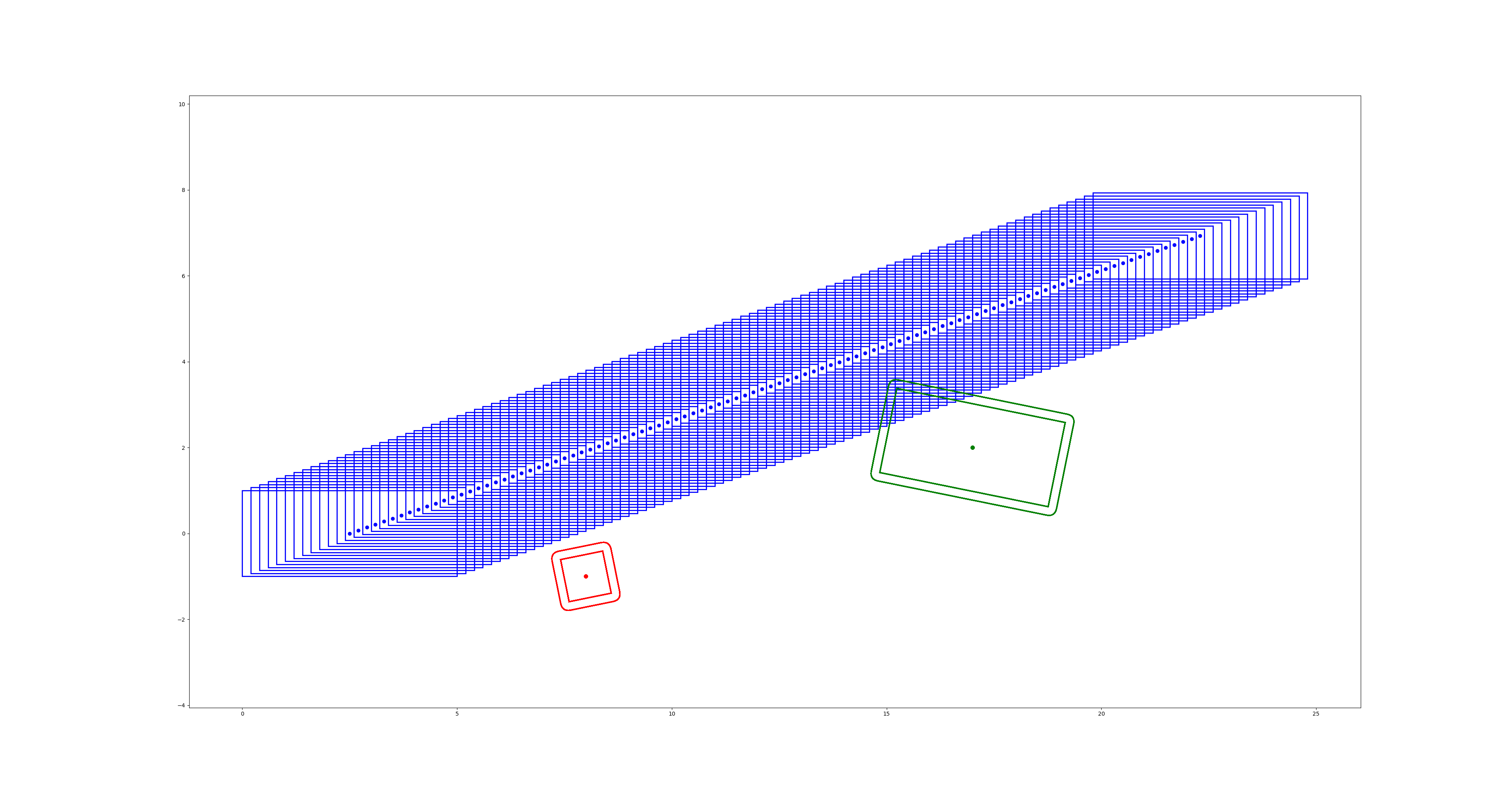 最优轨迹:
最优轨迹:

初始解:
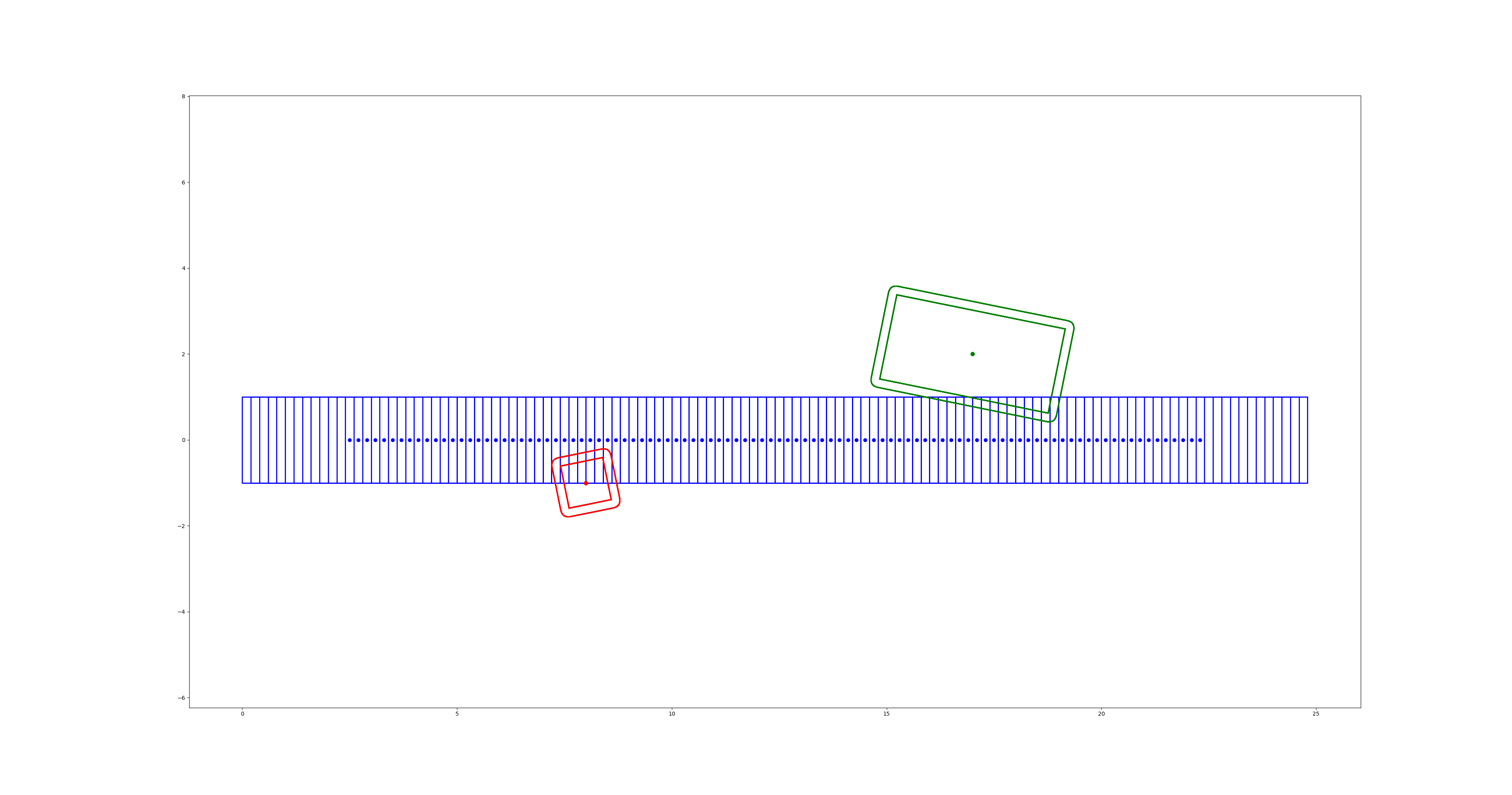 最优轨迹:
最优轨迹:
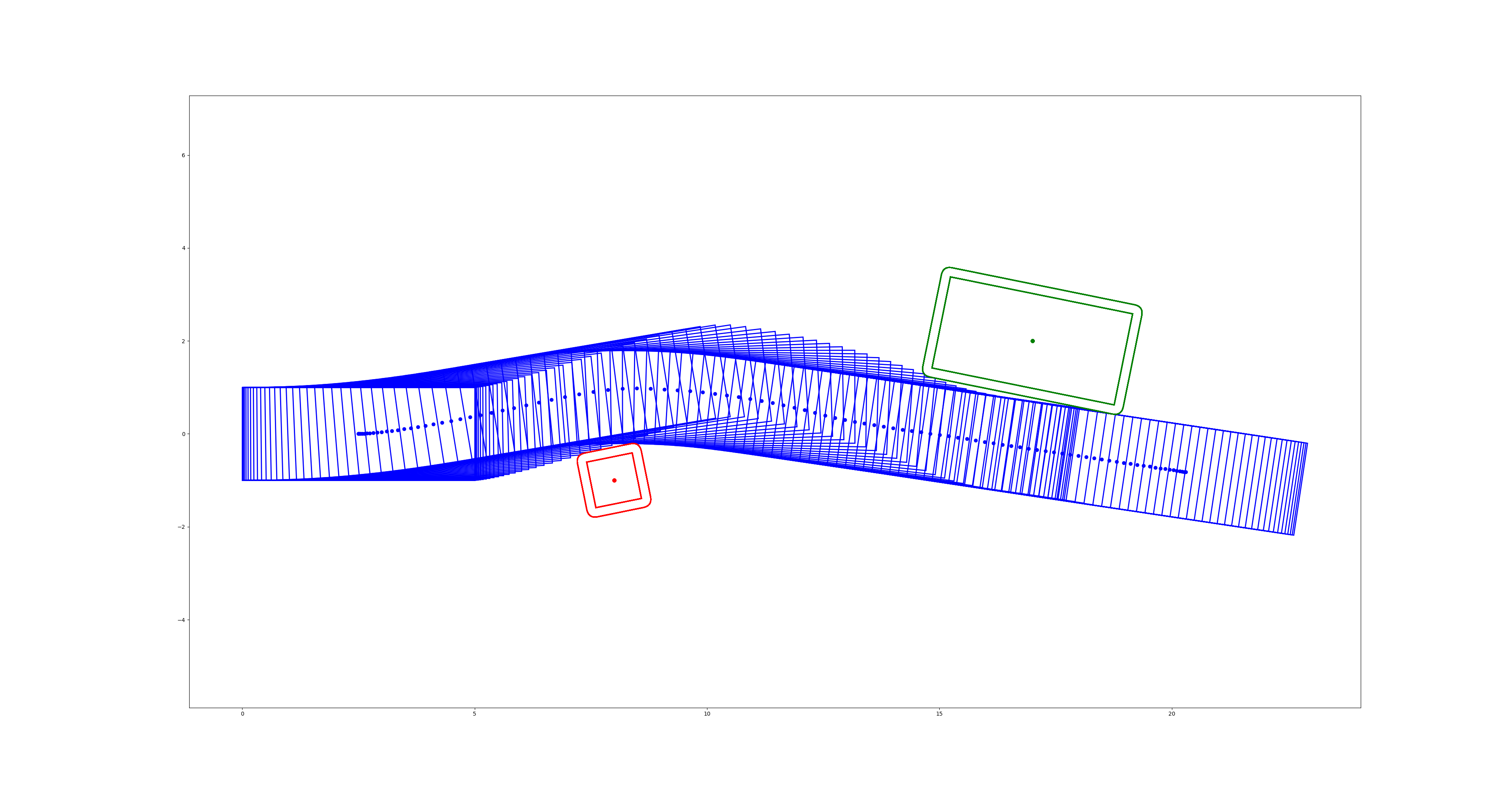
初始解:
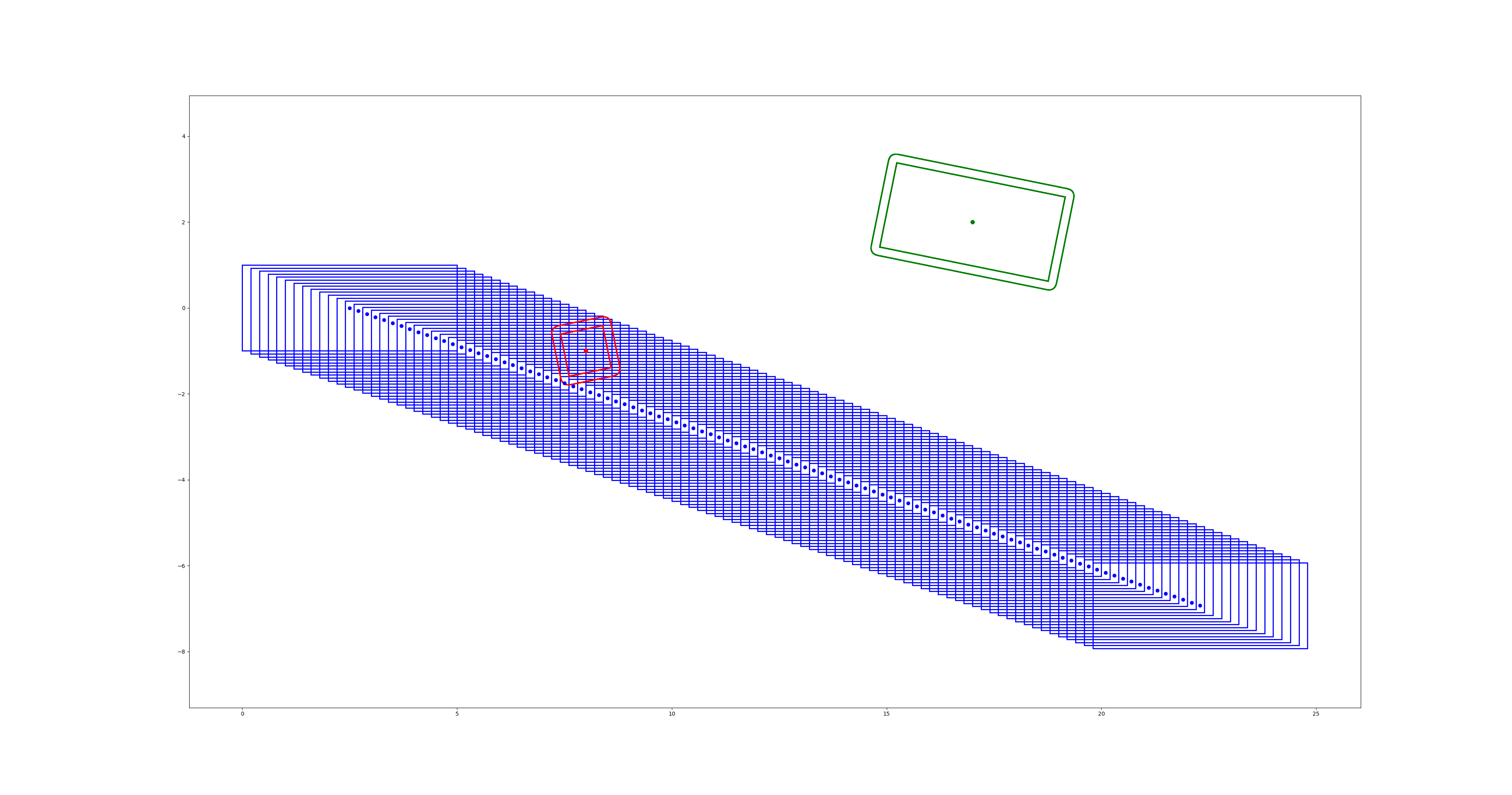 最优轨迹 (受最大转角约束限制, 求解器返回
最优轨迹 (受最大转角约束限制, 求解器返回solve_status = 3的不可行标志位与最小约束违反解):